好了，做完了單狹縫，當然要來玩雙狹縫！

今天就來建立在昨天單狹縫的基礎上去修改，如下：

import numpy as np
import matplotlib.pyplot as plt

#定義雙狹縫
def double_slit_x(spacing): #spacing狹縫間隔
    return [-spacing/2, spacing/2] #以0為中心的間隔

D = 10 #繪圖範圍-5~5
d = 1  #狹縫寬度
N = 501 #繪圖間隔（精度）
spacing = 1
x_list = double_slit_x(spacing)
source = [1 for i in range(len(x_list))]  #將x_list和光source長度統一

def phase_term(kx, x): #處理complex，也就是公式中dx以前的部分
    phase = complex(0, -kx*x) #前面放實部（這裡面沒有，所以為0），後面為虛部-kx*x
    return np.exp(phase) #呼叫exponential e的i次方

def Fraunhofer_1D(kx, source, x_list, dx): #dx就是D/N(寬)，source帶入phase term就是每段高度做積分
    output = 0
    for i in range(len(x_list)):
        rec_area = source[i]*phase_term(kx, x_list[i])*dx #黎曼和長方形面積
        output += rec_area  #不斷地跑回圈加長方形面積
    return output

K = 2*np.pi*10 #波數
kx_list = [-K/2 + K*i/N for i in range(N)] #波數(空間上的分佈)
far_field = [Fraunhofer_1D(kx_list[i], source, x_list, 1) for i in range(N)] #1是兩個波源相加的結果
intensity = [abs(far_field[i])**2 for i in range(N)]

plt.plot(kx_list, intensity, color = 'skyblue')
plt.title('1DFourierTransform_single_slit')
plt.ylabel('Intensity')
plt.legend()
plt.show()

可以看到有改動的只有：

1. 雙狹縫的定義
2. spacing, x_list, source增訂與改動
3. K數據微調，為了出圖效果明瞭。
4. far_field中帶入Fraunhofer算式的dx改為1 (Δx=1 是一種簡化處理，用來表示兩個波源相加後的建設性干涉結果。這樣可以方便地分析雙狹縫中的干涉現象。)

得出圖如下—

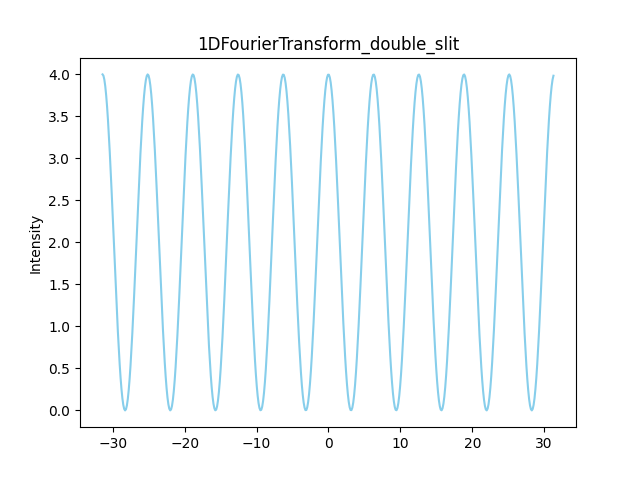
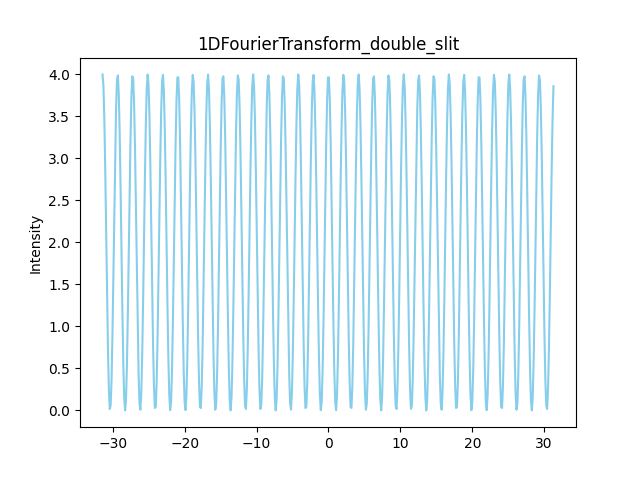
如果將雙狹縫的間距拉開
Spacing = 3

可以看到光強度變化變密集—

以上程式碼是課程助教教學分享內容，我則是利用chatGPT對我解釋變更內容，再自己默默消化...

（非理科的我真的消化不良了QQ）

其中我試著在裡面加入x_list對far_field和source的圖，但卻遇到虛部被省略的狀況，而我問了chatGPT得出的答案非常模稜量可，再不確定是否可以省略的狀態下，就不放在途中和程式裡和大家分享了。

不過，至少視覺上我還是能多少理解其中內涵，希望有路過大神可以幫我深入解釋～